Anhang 2

Bemessung der Abblaseleistung von Sicherheitsventilen bei Wärmeeintrag in ortsfeste Druckgasbehälter für verflüssigte Gase infolge Wärmeeinstrahlung

(1) Diese Anlage gilt für verflüssigte Gase, da nur für diese bei zu erwartendem Wärmeeintrag ggf. erhebliche Abblaseleistungen der Sicherheitsventile erforderlich sein können.

(2) Wird bei ortsfesten Druckgasbehältern die zulässige Betriebstemperatur (höchstmögliche Temperatur des enthaltenen Gases), z. B. durch Wärmestrahlung bei einem Brand, überschritten, so wird aufgrund des Anstieges des Dampfdruckes des Gases der Ansprechdruck des Sicherheitsventiles überschritten. Die höchsten Temperaturen stellen sich – abhängig vom Wärmeeintrag – an der nicht mit verflüs-sigtem Gas gekühlten Behälteroberfläche ein, da an diesen Stellen eine Wärmeab-fuhr nur durch die Gasphase erfolgt. An diesem Teil der Behälterwandung darf höchstens die zulässige Werkstofftemperatur erreicht werden. Diese Temperatur ergibt sich aus der Berechnung mit dem Sicherheitsbeiwert S = 1 gegen die Streck-grenze (siehe Anhang 3 Tabelle 1). Abgeleitet aus den geometrischen Verhältnissen bei der Bestrahlung eines Behälters mit einer Wärmequelle und der konservativen Annahme, dass

• auf den Druckgasbehälter nur Wärme einstrahlt, keine Wärme durch Strahlung oder Konvektion abgegeben wird und
• der Druckgasbehälter auf der Querschnittsfläche A = d ∙ l gleichmäßig mit dem hohen Wert der senkrechten Einstrahlung am Äquator bestrahlt wird,

erhält man aus der Wärmebilanz den entsprechenden verdampfenden Massestrom des verflüssigten Gases. Diesen Massestrom muss das Sicherheitsventil in der Lage sein abzuführen. Mit weiteren Annahmen zur sicheren Seite hin, erhält man folgende Gleichung:

mit

Stellt man die Gleichung um zu

erhält man das Diagramm gemäß Abbildung 4.

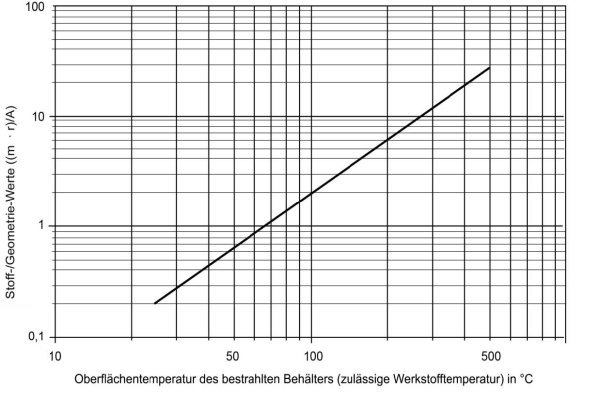
Abbildung 4: Mengenbemessung für die Abblaseleistung von Sicherheitsventilen bei durch Wärmestrahlung beaufschlagten Behältern

(3) Ergeben sich danach zu große Sicherheitsventile, so ist eine genauere Berechnung mit den entsprechenden Randbedingungen erforderlich.

Für weitere Informationen siehe z. B.

1. Gas-Wärme-Institut, Bericht Nr. 8112 vom 9.4.1990, "Brandlast/Strahlungs-versuche zur Ermittlung von Mindestabständen von Druckbehältern für Flüssig-gas nach DIN 51622 zu möglichen Brandherden".
2. Technische Überwachung, BD 32 (1991), Nr. 4, S. 142 ff., "Lagerung brennbarer Stoffe – Berechnung von erforderlichen Abständen zu möglichen Brandlasten".
3. "Flüssiggas" Heft 5/91, Strobel-Verlag Arnsberg – Brandlast-/Strahlungsversuche (Metzger) – Berechnung von erforderlichen Abständen zu möglichen Brandlasten (Becker, Huth, Müller).

(4) Die nachfolgenden Beispiele erläutern die Berechnung der erforderlichen Ab-blaseleistung eines Sicherheitsventils an einem Lagerbehälter für Propan und an ei-nem Lagerbehälter für Ammoniak.

Beispiel 1 Lagerbehälter für Propan

Die hypothetische Brandlast soll zu der zulässigen Werkstofftemperatur (Oberflä-chentemperatur im Bereich der Gasphase) von 250 °C am Lagerbehälter führen, was bei

• Bemessung des Abstandes zur Brandlast nach Anhang 3,
• Dauerbelastung durch die Wärmestrahlung und
• abblasendem Sicherheitsventil

eine Temperatur von 42 °C in der Flüssigphase des Gases ergibt (s. GWI-Bericht; die Kühlung durch Verdampfung des Gases hält die Flüssigphase auf der Tempera-tur von 42 °C; bei einer Bemessung des Sicherheitsventils mit den oben zugrunde gelegten Vorgaben ist immer eine dem Abblasedruck des Gases – d. h. dem Ein-stelldruck des Sicherheitsventils – entsprechende Temperatur gegeben).

Aus der Gleichung bzw. dem Diagramm ergibt sich bei 250 °C

Daraus folgt die über das Sicherheitsventil abzuführende Menge mit

Beispiel 2 Lagerbehälter für Ammoniak

Die hypothetische Brandlast soll zu der zulässigen Werkstofftemperatur von 260 °C am Lagerbehälter führen (s. a. Erläuterung in Beispiel 1).

Aus der Gleichung bzw. dem Diagramm ergibt sich bei 260 °C

Daraus folgt die über das Sicherheitsventil abzuführende Menge mit